Understand Tensor Data Layout

Summary

This article introduces the two common memory storage formats in PyTorch, NCHW and NHWC. It delves into concepts such as Stride and Contiguous, and explains the principles and processes of changing Tensor memory structures.

Introduction

Suppose there is a Tensor X in NCHW format, with X.shape = [1, 64, 5, 4], arranged in row-major order, as shown in the figure below

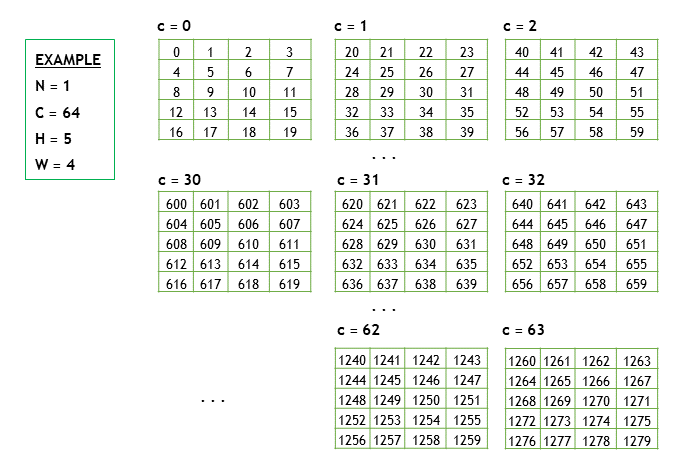
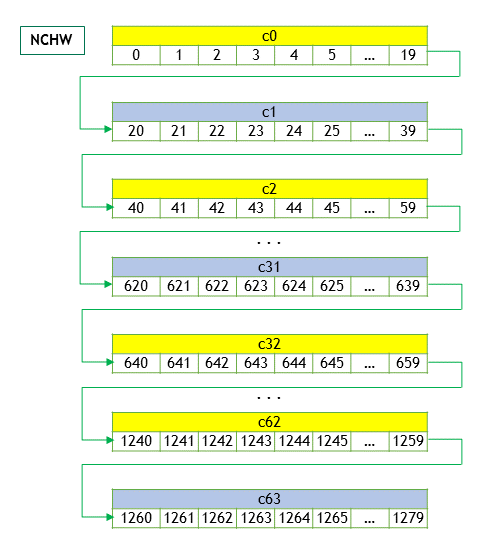
The memory layout is as shown in the figure (priority access to W, H, then the channel C +=1)

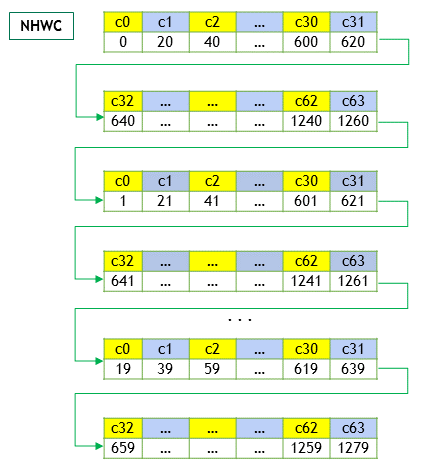
If it is arranged in the form of NHWC, then it will change to (priority access to data from different channels, then W, H+=1)

Introduction to Stride, Contiguous

1
2
3
4
5
6
7

import torch

N, C, H, W = 1, 64, 5, 4
x = torch.rand(N, C, H, W)
print(x.shape)              # torch.Size([1, 64, 5, 4])
print(x.stride())           # (1280, 20, 4, 1)
print(x.contiguous())       # True

Stride is the step length that needs to be taken in memory, and its calculation method is as follows

1
2
3
4
5

size_t stride = 1;
for (int i = ndim_ - 1; i >= 0; i--) {
    stride_[i] = stride;
    stride *= shape_[i];
}

For example, to take the next value of H, we know to traverse 4 row elements (W=4), then we can get this value directly according to stride[2]=4, and add 4 to the memory pointer to get the element we need. Again, to take the next C, just add 20 to the memory pointer to get the corresponding value.

Contiguous refers to whether the memory space layout is continuous. Because we prioritize rows, it complies with the definition of continuity if we can access in the order of rows. The code to determine whether it is continuous is as follows:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

bool is_contiguous() const {
    size_t stride = 1;
    for (int i = ndim_ - 1; i >= 0; i--) {
        if (stride_[i] != stride) {
        return false;
        }
        stride *= shape_[i];
    }
    return true;
}

In general, operations on tensors (such as transpose, permute, etc.) only change the description of the tensor (shape, stride) and do not change the actual memory structure of the tensor. For example:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

import torch

N, C, H, W = 1, 3, 2, 2
x = torch.randint(1, 30, (N, C, H, W))
print(x.is_contiguous())        # True
print(x.storage())              # [25, 29, 28, 6, 12, 25, 4, 20, 17, 21, 19, 5]
print(x.shape)                  # torch.Size([1, 3, 2, 2])
print(x.stride())               # (12, 4, 2, 1)
x = torch.transpose(x, 0, 2)
print(x.is_contiguous())        # False
print(x.storage())              # [25, 29, 28, 6, 12, 25, 4, 20, 17, 21, 19, 5]
print(x.shape)                  # torch.Size([2, 3, 1, 2])
print(x.stride())               # (2, 4, 12, 1)

However, changing the memory format not only changes the description of the tensor, but also needs to directly change the storage of the tensor. The conversion between NCHW and NHWC below shows the process.

Conversion between NCHW and NHWC

1
2
3
4
5
6
7
8

import torch

N, C, H, W = 1, 64, 5, 4
x = torch.rand(N, C, H, W)
x = x.contiguous(memory_format=torch.channels_last)
print(x.shape)              # torch.Size([1, 64, 5, 4])
print(x.stride())           # (1280, 1, 256, 64)
print(x.is_contiguous())    # False

As can be seen, the shape has not changed, but the stride has changed from (1280, 20, 4, 1) to (1280, 1, 256, 64)

How did this stride change occur? Please see the code below

1
2
3
4
5

int64_t stride = 1;
for (auto k : {1, 3, 2, 0}) {
    strides[k] = stride;
    stride *= shapes[k];
}

That is, elements on C are accessed first, then W, H are accessed, and finally N is accessed.

How is this priority access implemented through stride? First, we need to understand how tensor gets values

1
2
3
4
5
6
7
8

// get value by indexs
data_t operator[](std::vector<size_t> idxs) const {
    size_t offset = 0;
    for (size_t i = 0; i < ndim_; i++) {
        offset += idxs[i] * stride_[i];
    }
    return data_[offset];
}

For example, when a user accesses tensor_channel_last[0,1,0,0] data and wants to get the next c value, then offset = 1280 * 0 + 1 * 1 + 256 * 0 + 64 * 0 = 1, which just got the data at offset=1

This raises a question. Doesn’t the data pointer offset=1 point to the value of w=1? Therefore, after changing to channel-last, the layout of data on the one-dimensional array in memory also changes to fit the offset.

Let’s take a smaller tensor to analyze the memory layout

1
2
3
4
5
6
7

import torch

N, C, H, W = 1, 3, 2, 2
x = torch.randint(1,30,(N, C, H, W))
print(x.storage())  # [ 14 16 20 11 8 26 15 18 29 21 10 3]
x = x.contiguous(memory_format=torch.channels_last)
print(x.storage())  # [ 14 8 29 16 26 21 20 15 10 11 18 3]

It can be seen that the original index 4 is 8 (corresponding to c1h0w0), and now the index has changed to 1, which is just adapted to the new stride.

Why Distinguish and Convert Between NCHW and NHWC - Performance Improvement

In some operator computations, it is actually necessary to get the next dimension C. If you follow the continuous method, the offset is H*W. Although the value is still O(1), it cannot hit the cache, resulting in performance degradation. After converting to NHWC, it becomes very convenient to get the value of C every time.

According to the PyTorch documentation, when used with AMP (Automated Mixed Precision), it can achieve a 22% performance increase on NVIDIA GPUs. Even on CPUs, performance can be improved due to better cache hits.

Reference

• NVIDIA Deep Learning cuDNN Documentation
• Pytorch NCHW/NHWC
• (BETA) CHANNELS LAST MEMORY FORMAT IN PYTORCH