CSAPP Class Notes(1)

Summary

My note while learning through CSAPP-15213 videos. Including Overview, Bits,Bytes, and Integers, Floating Point, Machine Level Programing, Program Optimization and Memory. Source: Github-Link-Here

1. Overview

Course theme

• theme：Abstraction is good but don’t forget reality

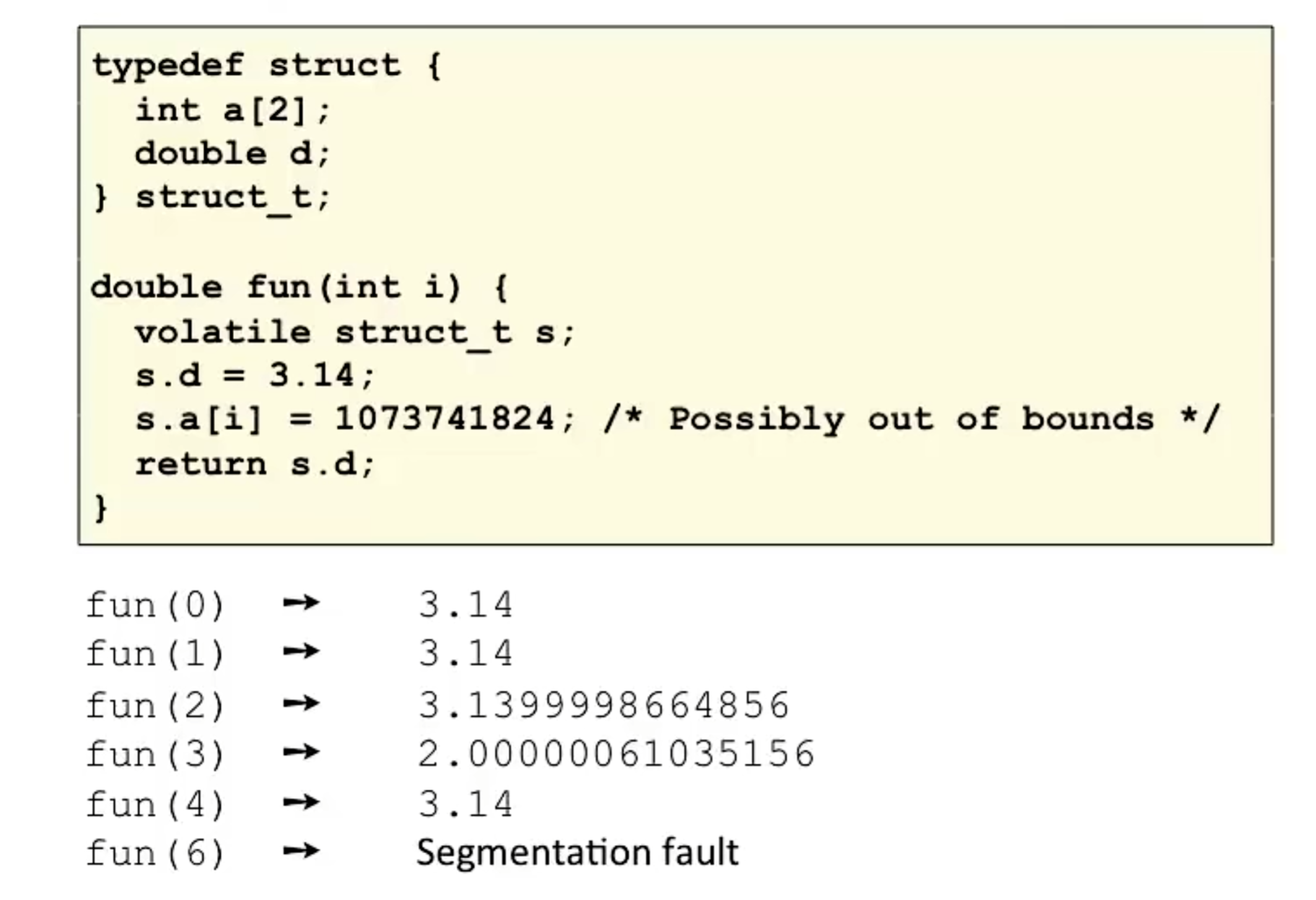
Five realities

• ints are not integers；floats are not real
  • To understand numbers in computer
  • eg：x^2 >= 0?
    • for float：yes！
    • for int： 40000*40000=1600000000 yes! 50000*50000=?? not!
  • eg：(x+y) + z = x+(y+z)?
    • for int: yes!
  • for于 float: (1e20+-1e20)+3.14 = 3.14； (1e20+(-1e20+3.14) = ??
• you’ve got to know assembly
  • learning about assembly
• memory matters
  • memory management
  • eg：

    

• there’s more to performance than asymptotic complexity
  • eg：

    

• computers do more than execute programs
  • IO/network

How the course fits into the CS/ECE curriculum

build up the base for another courses.

Course architecture

• programs and data

  • L1(datalab): manipulating bits
  • L2(bomblab): defuse a binary bomb
  • L3(attacklab): injection attacks

• memory hierarchy

  • L4(cachlab): build a cache simulator

• Exceptional control flow

  • L5(tshlab): write a shell

• Virtual memory

  • L6(malloclab): write a malloc package

• networking and concurrency

  • L7(proxylab): write a web proxy

2. Bits,Bytes, and Integers

Representing information as bits

• Everything is bits.
• Encoding Byte values.

Bit-level manipulations

• Boolean Algebra
• Bit-level options in C: & | ~ ^
• Logic Operations in C: && || !
• Shift operations
  • eg:

    

Integers

Unsigned and signed

• Numeric ranges
  • signed: Tmax, Tmin
  • unsigned: Umax, Umin

Conversion, casting

• B2T, T2B
• B2U, U2B
• U2T, T2U
• Note: if both signed and unsigned in one expression, signed value implicitly cast to unsigned.
  • eg: for(int i = n; i-sizeof(char); i--) {} // run forever!
• Corner case: normally -(-x) = x, but -Tmin(-32) != Tmax(31) (number is in 5 bits)

Expanding, truncating

• expanding
  • eg: 1010(-6) -> 111010(-6)
• truncating
  • eg: unsigned: 11011(27) -> 1011(9) // mod 16
  • just remember: directly get the bytes then calculate it.

Addition, negation, multiplication, shifting

• addition(negation)

  • unsigned addition
  • complement addition
  • overflow

• multiplication

  • unsigned multiplication
  • signed multiplication
    • eg: 5 * 5 = 25:0001-1001(-7). the result is -7

• shift

  • power-of-2 multiply with shift
  • unsigned power-of-2 division with shift
    • eg: 0011(3) /2 (»1) = 0001(1)–logical shift
  • signed power-of-2 division:
    • eg: 1101(-3) /2 (»1) = 1110(-2)–arithmetic shift

• extra:

  • x -> -x, just do !x+1
    • eg: -(1010) (-6) = 0101+0001 = 0110(6)

Representations in memory, pointers and strings

• Byte-Oriented Memory Organization
• Machine words: 32bits, 64bits
• Word-Oriented Memory Organization
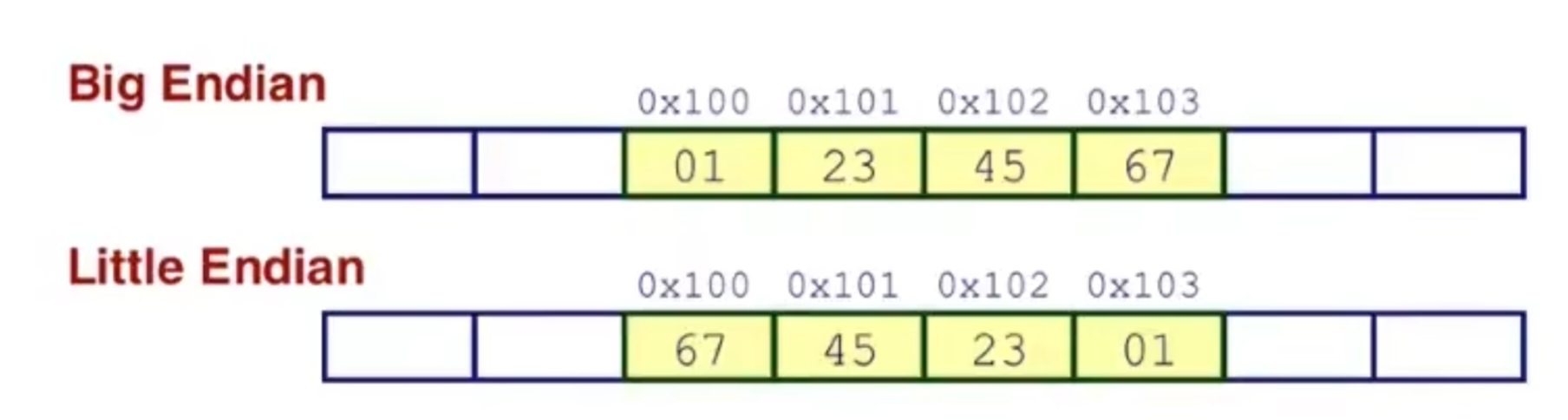
• Byte Ordering

  

3. Floating Point

Fractional binary number

eg:

• 5 + 3/4 = 101.11~2~
• 2 + 7/8 = 10.111~2~
• 1/3 = 0.0101[01]…~2~

IEEE Floating Point

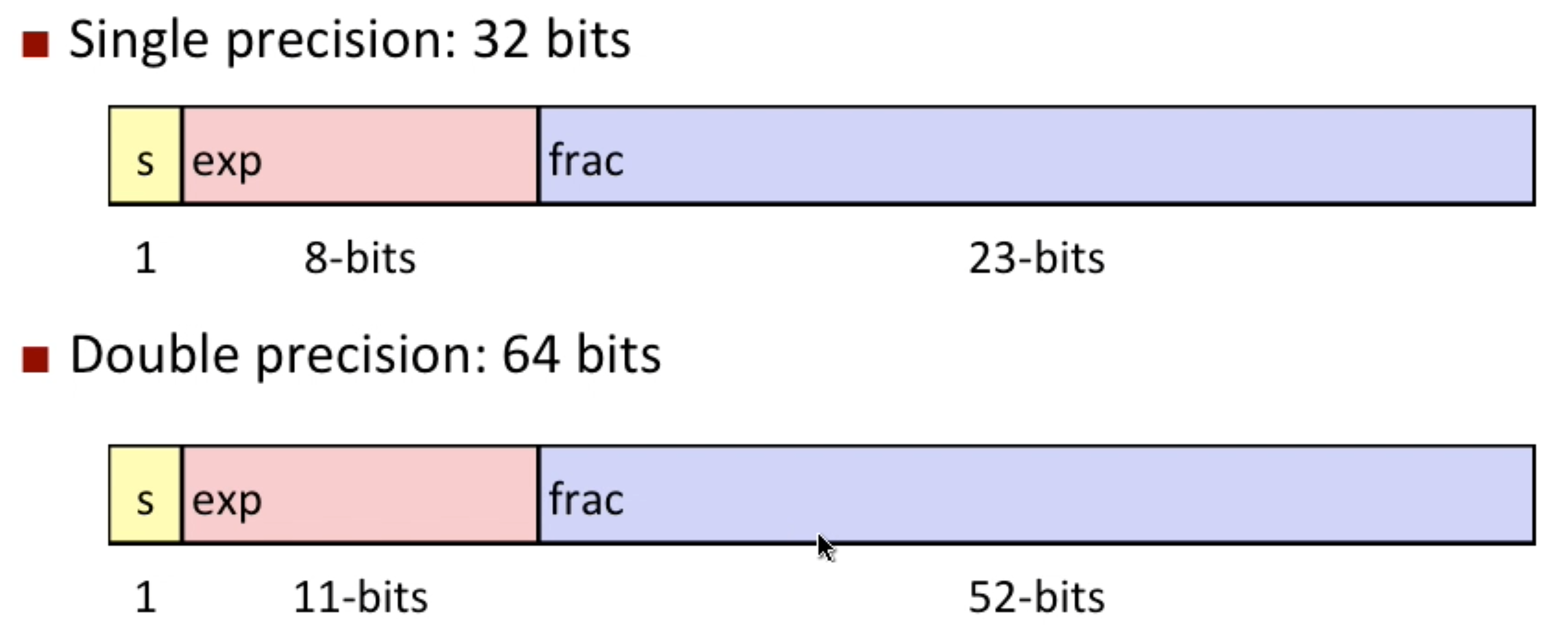
• f = (-1)^s^ M 2^E^

  • E = exp - Bias
    • eg. exp has 8 bits, Normally 1<=exp<=254, bias = 127, so -126<=E<=127
    • why introducing the bias? for better comparison
  • M = 1.0 + frac = 1.xxxx..x~2~
    • eg. minimum: xxxx..x = 0000..0, M = 1.0
    • eh. maximum: xxxx..x = 1111..1, M -> 2.0
  • Take 15123 as an example:
    • 15213 = 11101101101101~2~ = 1.1101101101101~2~ * 2^13^
    • M = 1.1101101101101~2~, frac = 1101101101101 + 0000000000
    • E = 13, bias = 127 -> exp = 140 = 10001100~2~
    • so result:
      • 0
      • 10001100
      • 1101101101101 0000000000
      • totally 32 bits

• For Denormalized Number: when exp = 00000..0

  • E = 1 - bias,
  • M = frac (no leading 1)
  • cases:
    • frac = 0000.0: representing 0 (including -0 and +0)
    • frac != 0000.0: closest to 0

• For Denormalized Number: when exp = 1111..1

  • E = 1 - bias,
  • M = frac (no leading 1)
    • why for this? to represent more numbers, see the figure below
  • cases:
    • frac = 0000.0: representing inf
    • frac != 0000.0: representing nan

• Examples together

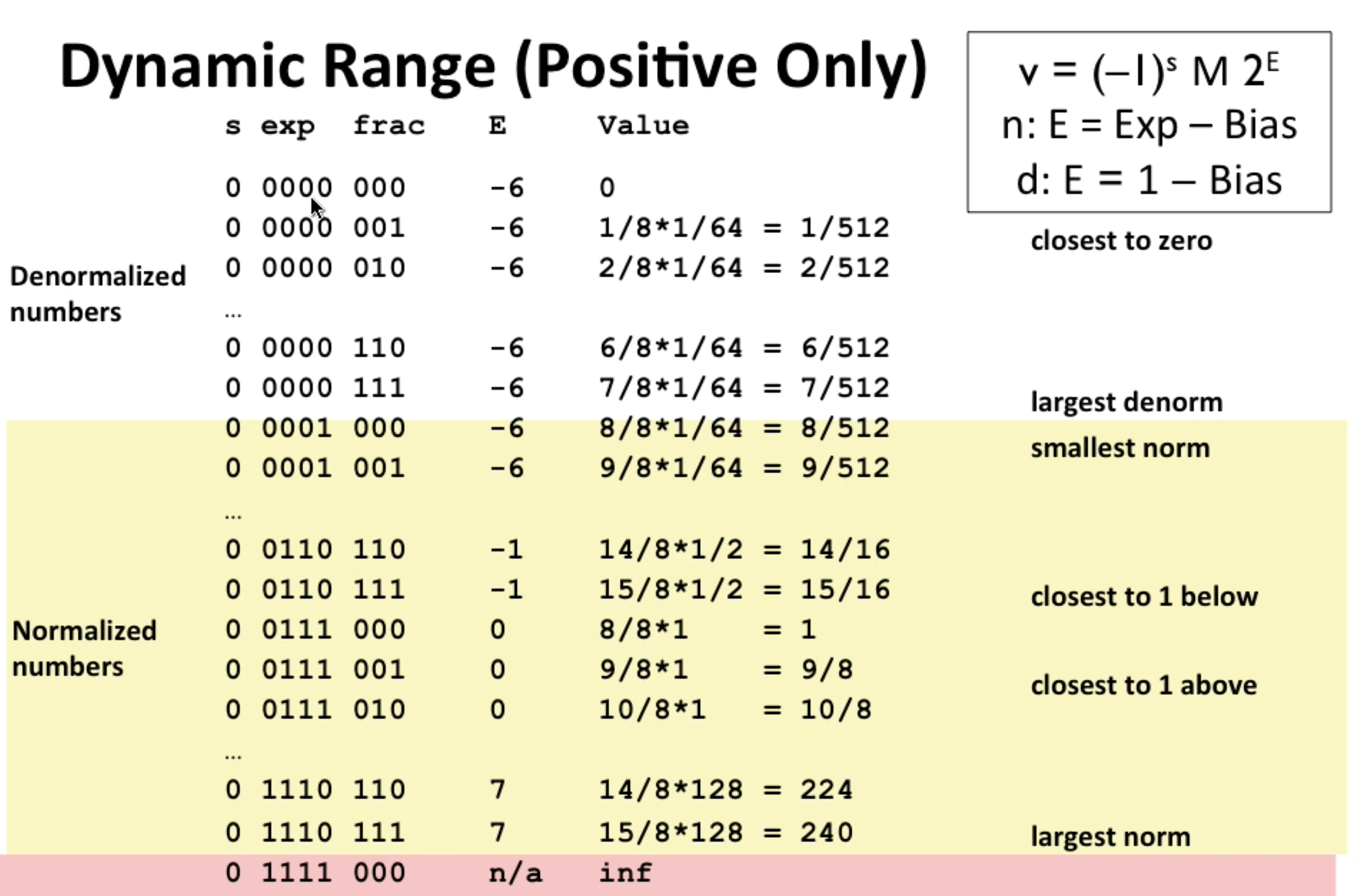
• Note: when closing to 0, the numbers get denser

Rounding, addition and multiplication

Round

• strategy

  • Towards 0
  • Round down(-inf)
  • Round up(+inf)
  • Nearest Even(default)

• eg: round to nearest 1/4

  • 2 + 3/16 = 10.00110~2~ = 10.01~2~ (>1/2 - UP)
  • 2 + 7/8 = 10.11100~2~ = 11.00~2~ (exactly half)
  • 2 + 5/8 = 10.10100~2~ = 10.10~2~ (exactly half)

multiplication

• (-1)^s1^ M1 2^E1^ * (-1)^s2^ M2 2^E2^

  • s = s1 ^ s2
  • M = M1 * M2
  • E = E1 + E2

• if after calculation,

  • M > 2 -> shift M right, increment E
  • If E out of range, overflow
  • Round M to fit frac

So now you understand why (1e20*1e20)*1e-20 = inf； (1e20*(1e-20*1e20) = 1e20

a>=b & c>=0 so a*c >= b*c? Almost, Always consider inf and nan

addition

core: get binary points lined up

• (-1)^s1^ M1 2^E1^ + (-1)^s2^ M2 2^E2^

• if after calculation,

  • M > 2 -> shift M right, increment E
  • M < 1 -> shift M left, decrement E
  • If E out of range, overflow
  • Round M to fit frac

So now you understand why (1e20+-1e20)+3.14 = 3.14； (1e20+(-1e20+3.14) = ??

Floating point to C

int -> float: round 32 bits value to 23 bits frac

double -> int: round 52 bits frac to 32 bits

2/3 != 2/3.0 (floating point)

double d < 0 -> d*2 <0 (YES! even if overflow, it’s negative inf)

4. Machine Level Programing

C, assembly, machine code

The process of compiling C:

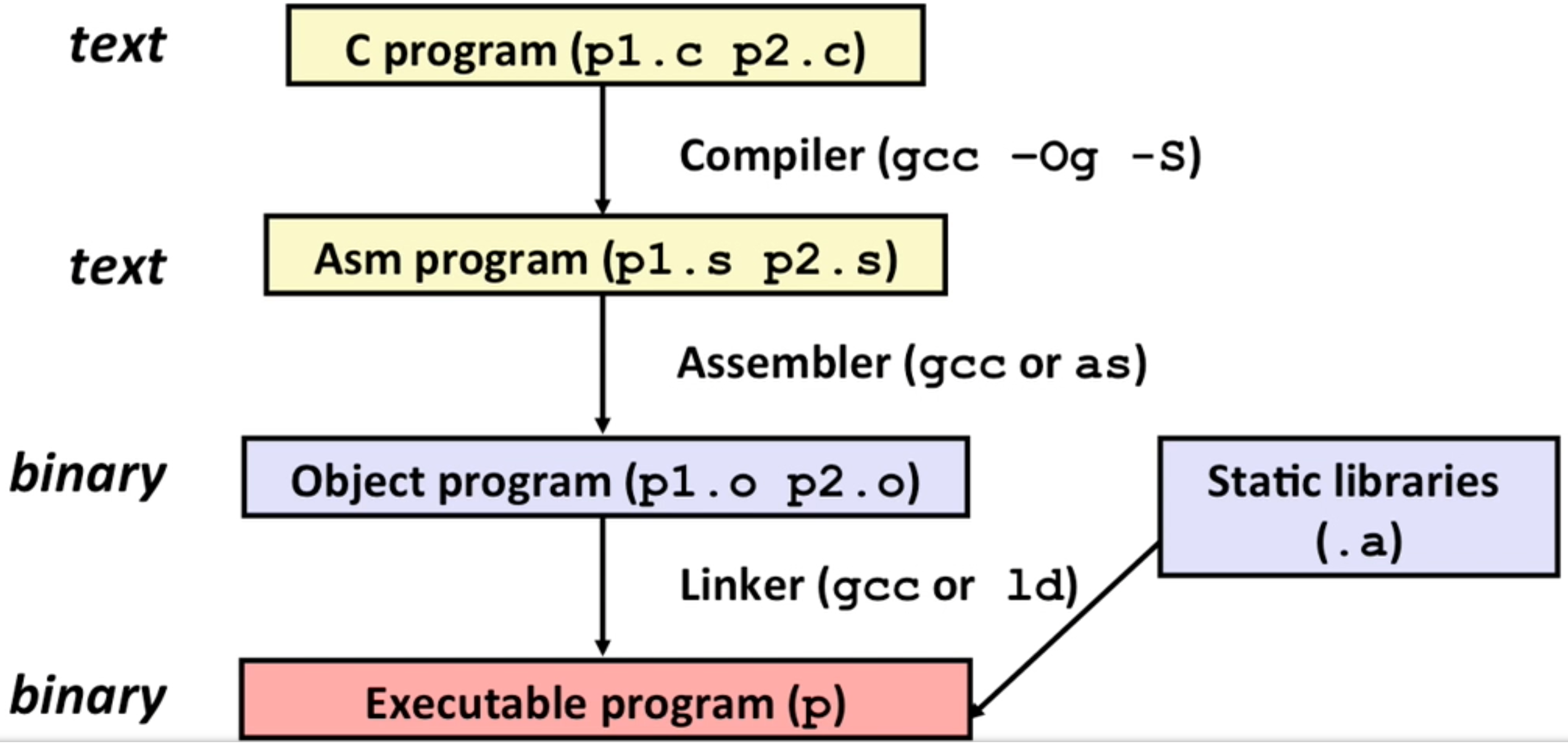
Compiler: GCC, to make assembly code: gcc -Og -S ...

to make exec file(actually bytes of instructions) into assembly code: objdump -d ...

Assembly Basics: Registers, operands, move

Some specific registers:

• %rsp: stack pointer
• %rdi: first argument of function
• %rsi: second argument of function
• %rdx: third argument of function

the relationships between different names of a register:

1
2
3
4
5

|63..32|31..16|15-8|7-0|
              | AH |AL |
              | AX.....|
       |EAX............|
|RAX...................|

Memory access of moveq:

• Normally: (%rax) = Mem[rax]
• With offset: 8(%rax) = Mem[rax + 8]
• Generally: D(Rb, Ri, S) = Mem[Rb + S * Ri + D]

Arithmetic & logical operations

For example: leaq

• leaq 4(%rsi, %rsi, 2), %rdx: rdx = rsi + 2 * rsi + 4

Control: Condition codes

• %rip: instruction pointer

• Condition Codes

  • CF(carry flag)–for unsigned overflow
  • ZF(zero flag)
  • SF(sign flag)–for signed
  • OF(overflow flag)– for signed overflow

• cmpq: compare number (b-a) and set condition codes above

• testq: compare number (a&b) but only set ZF and SF

• setX: set the low-order byte of destination to 0 or 1 based on the condition codes above

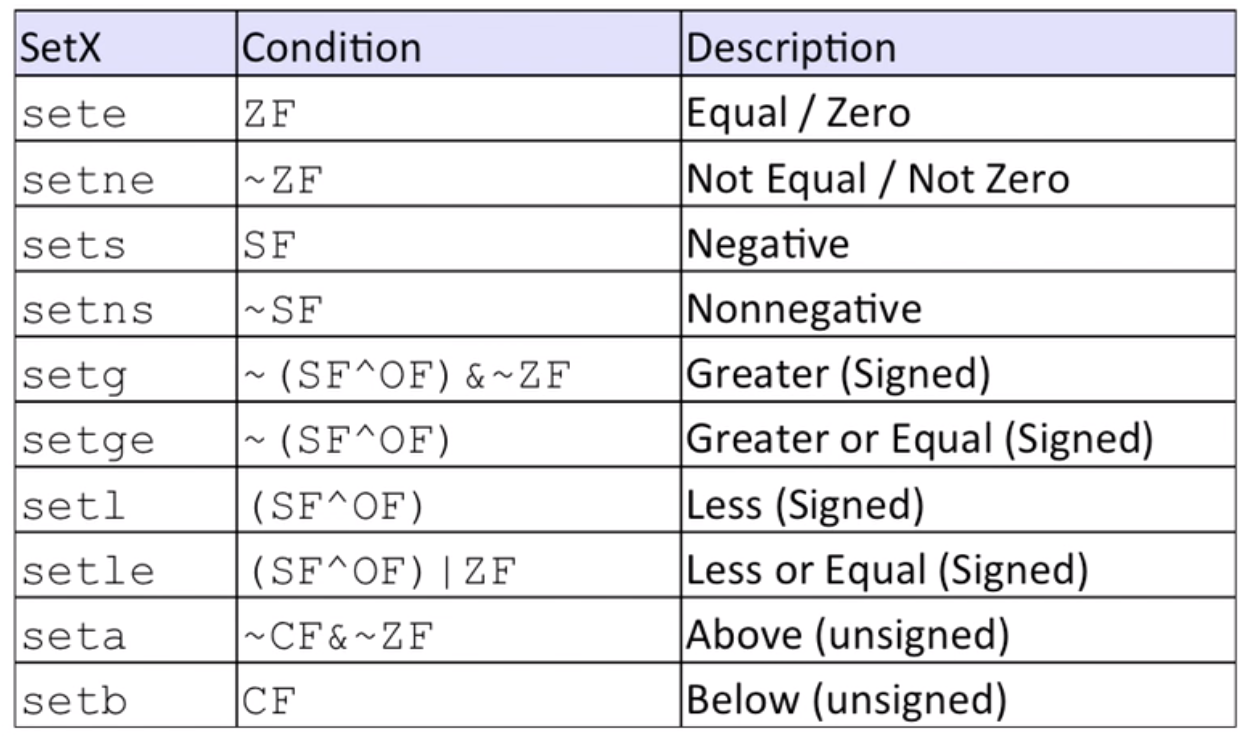
• example

1

int gt (long x, long y) {return x>y;}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

# compare x, y  (%rsi is y, %rdi is x)
cmpq    %rsi, %rdi

# Set when > (if x-y > 0, SF=1 and OF=1 or SF=0, OF=0)
setg    %al

# move bytes to long, zero padding
# Note this is %eax rather than %rax
# this is because 32-bit instructions also set upper 32 bits to 0.
movzbl  %al,  %eax
ret

Conditional branches

• jX: jump to different part of code depending on condition codes

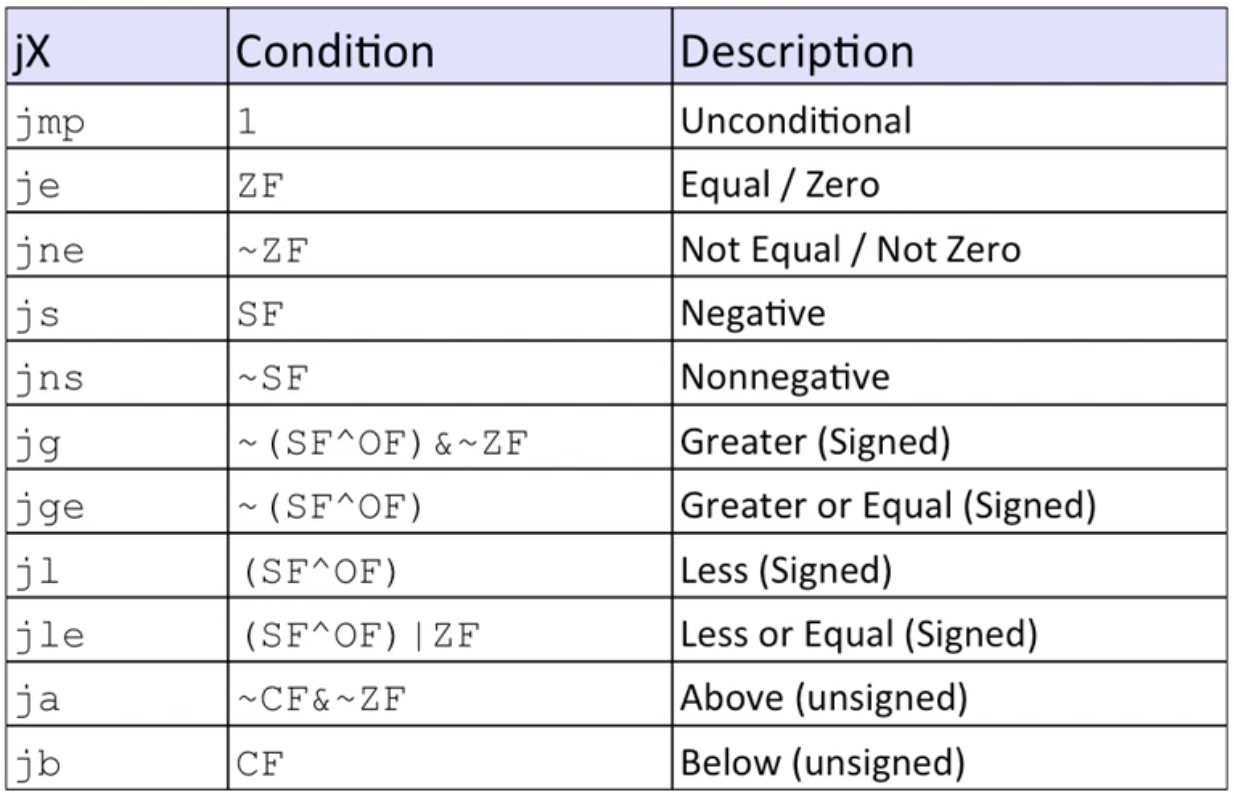
• Note: Sometimes like Test? x+y:x-y in C, it’s efficient to calculate x+y and x-y both, then choose one using conditional move rather than using branches. Since branches are very disruptive to instruction flow through pipelines

• conditional move

  • eg: cmovle %rdx %rax: if <=, result = %rdx
  • only use this when calculation is simple and is safe!

Loops

Using branches and control introduced above to realize do-while, while and for.

Switch Statements

• Structure:

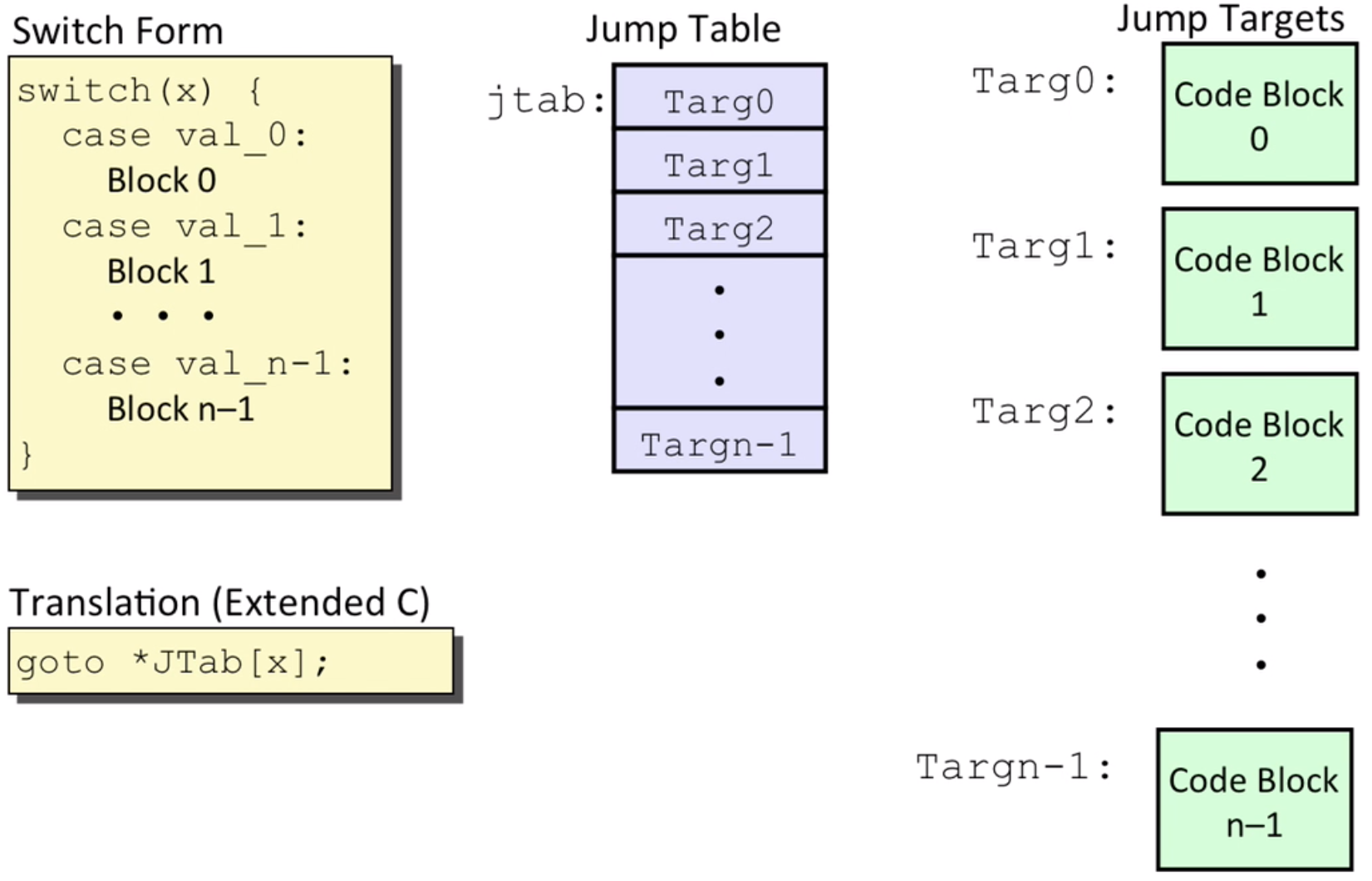
• How to form a jump table?

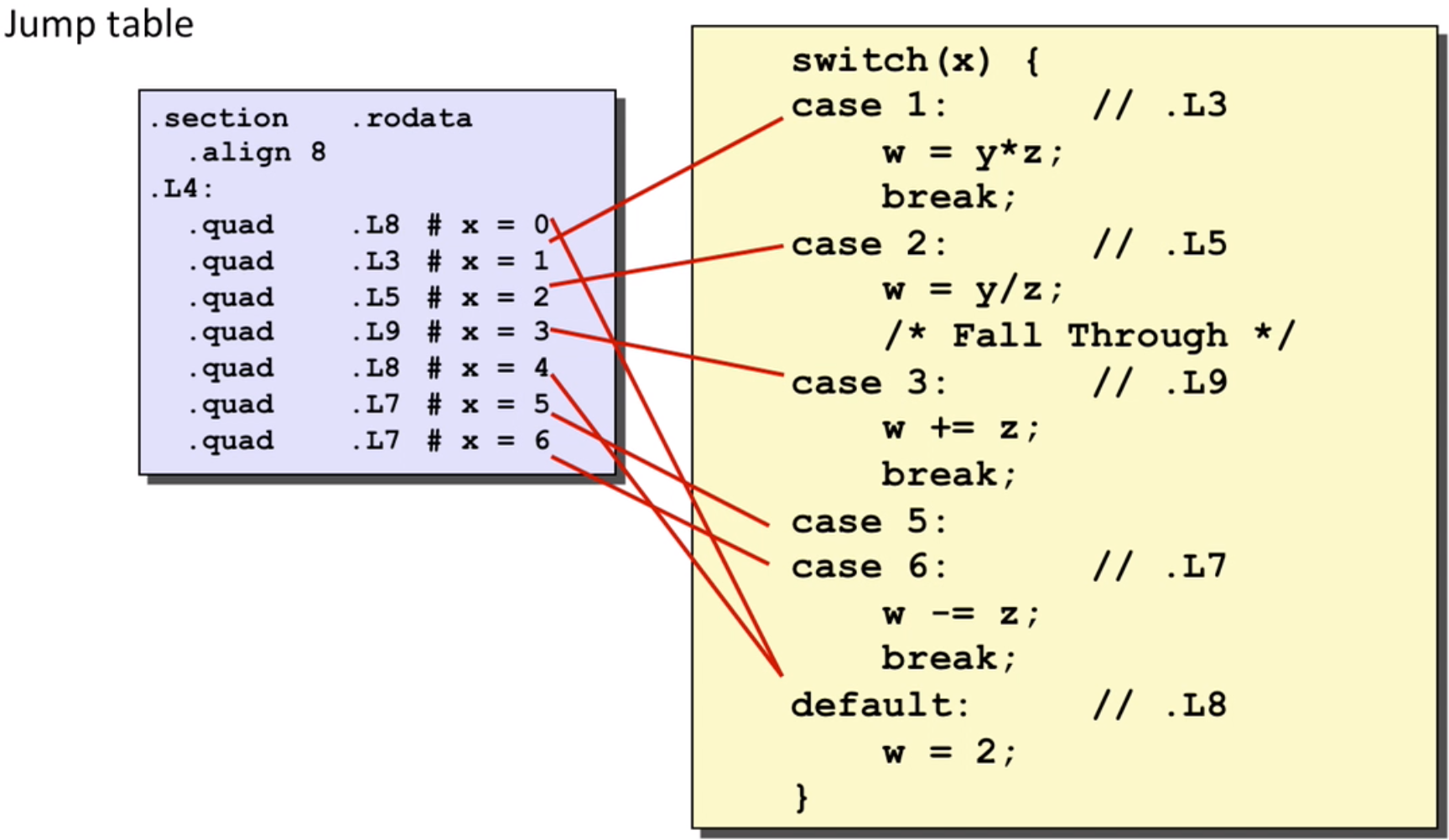
Normally to make an array, and for some holes like x=0, x=4, let it go to the default part.

Note: if x has a extremely large case like 10086, it can add a bias then make an array flow(like mapping to 7), too. Or sometimes it can be optimized to a decision tree–simple if else structure(in cases it’s hard to make an array flow)

• How to jump through table?

1
2
3
4
5
6
7
8
9

# x compare 6
cmpq $6, %rdi

# Use default: since we use **ja**(unsigned) here
# jump if x > 6 or x < 0(unsigned negative is a large positive)
ja   .L8

# refer to (L4 + 8 * %rdi) address, get the value of it and then jump
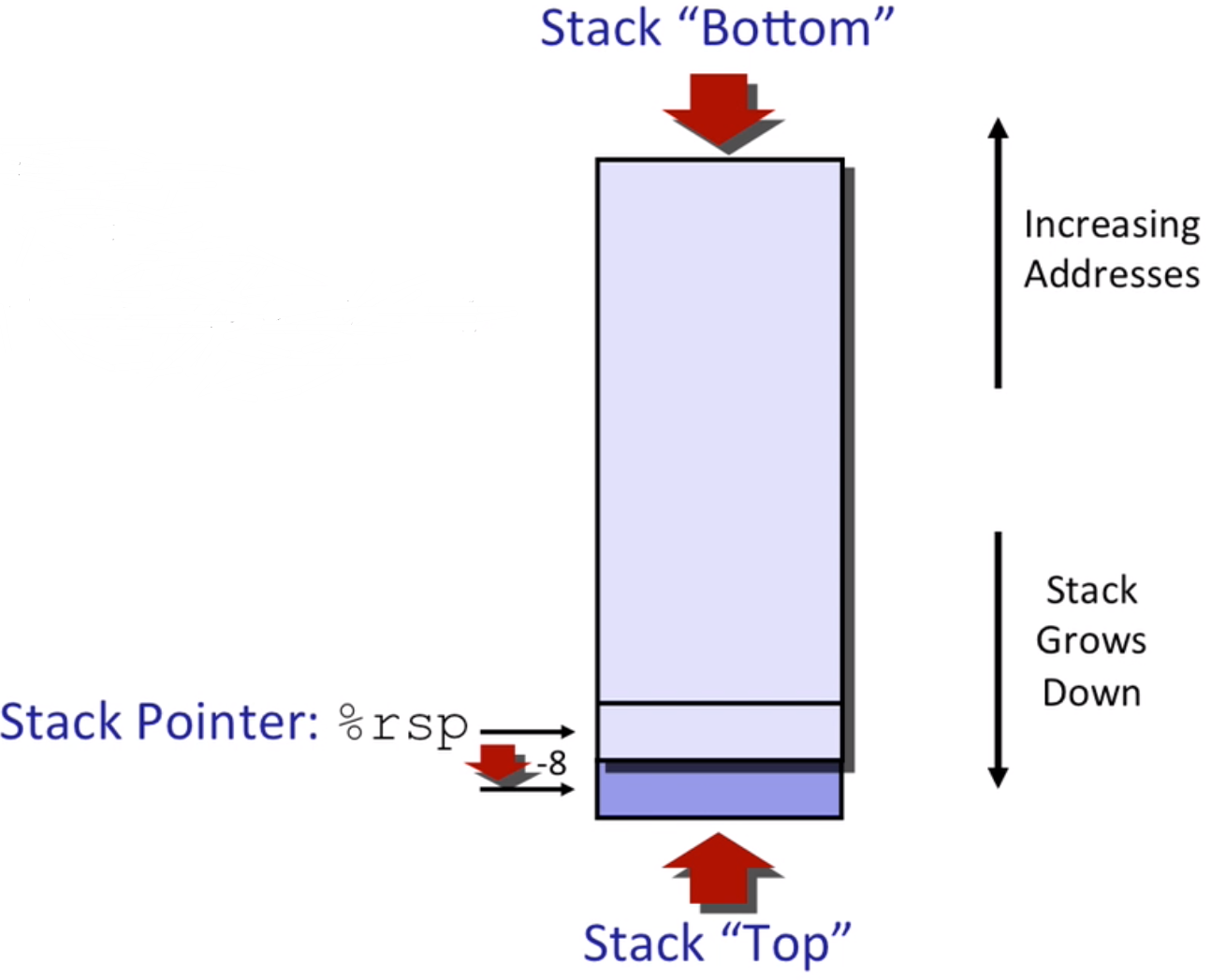
jmp *.L4(, %rdi, 8)

Stack Structure

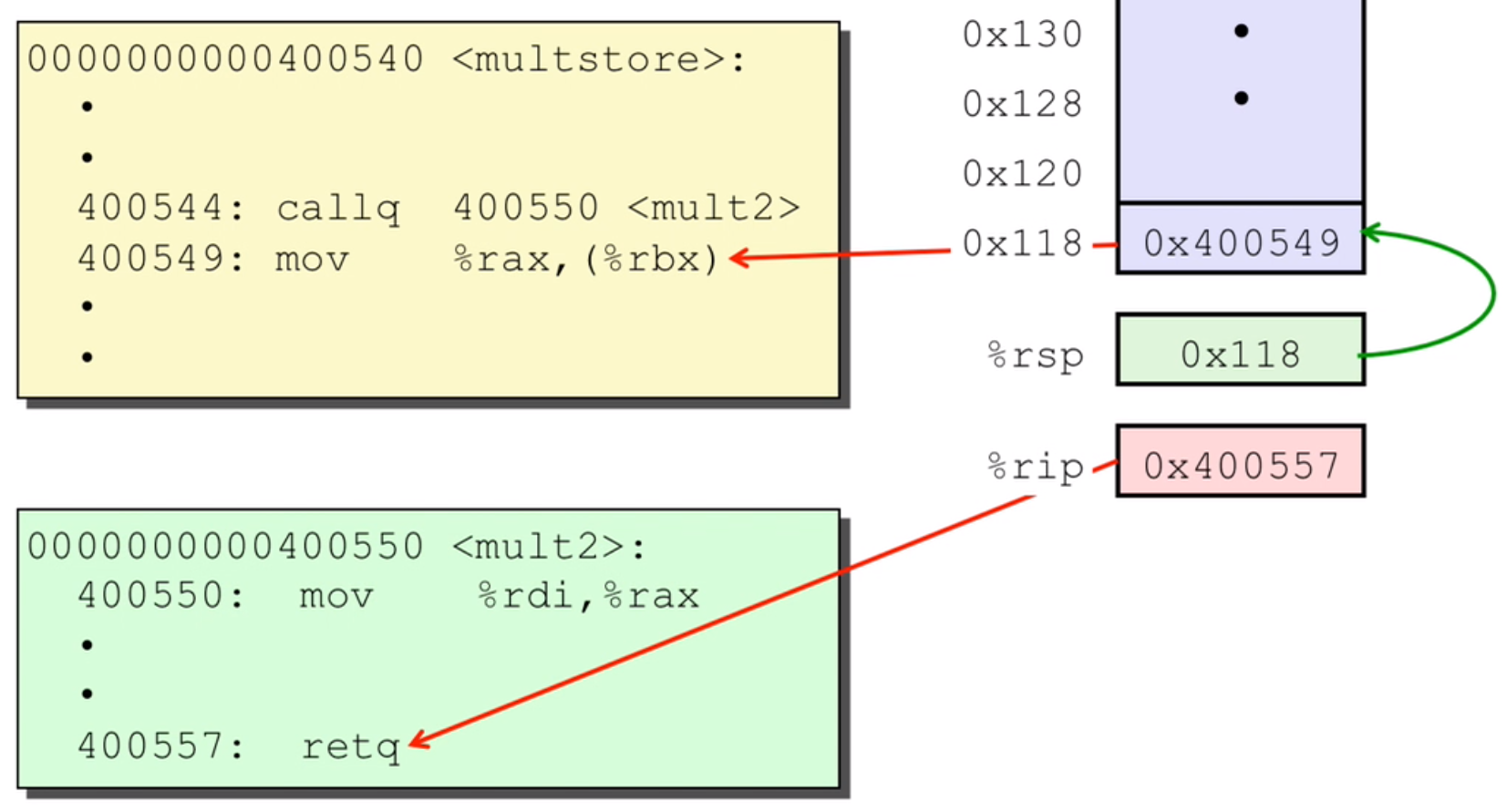
Calling Conventions

• passing control: when calling a function, push the next instruction address to the stack, when ret, get the address back then jump to the address.

• passing data:

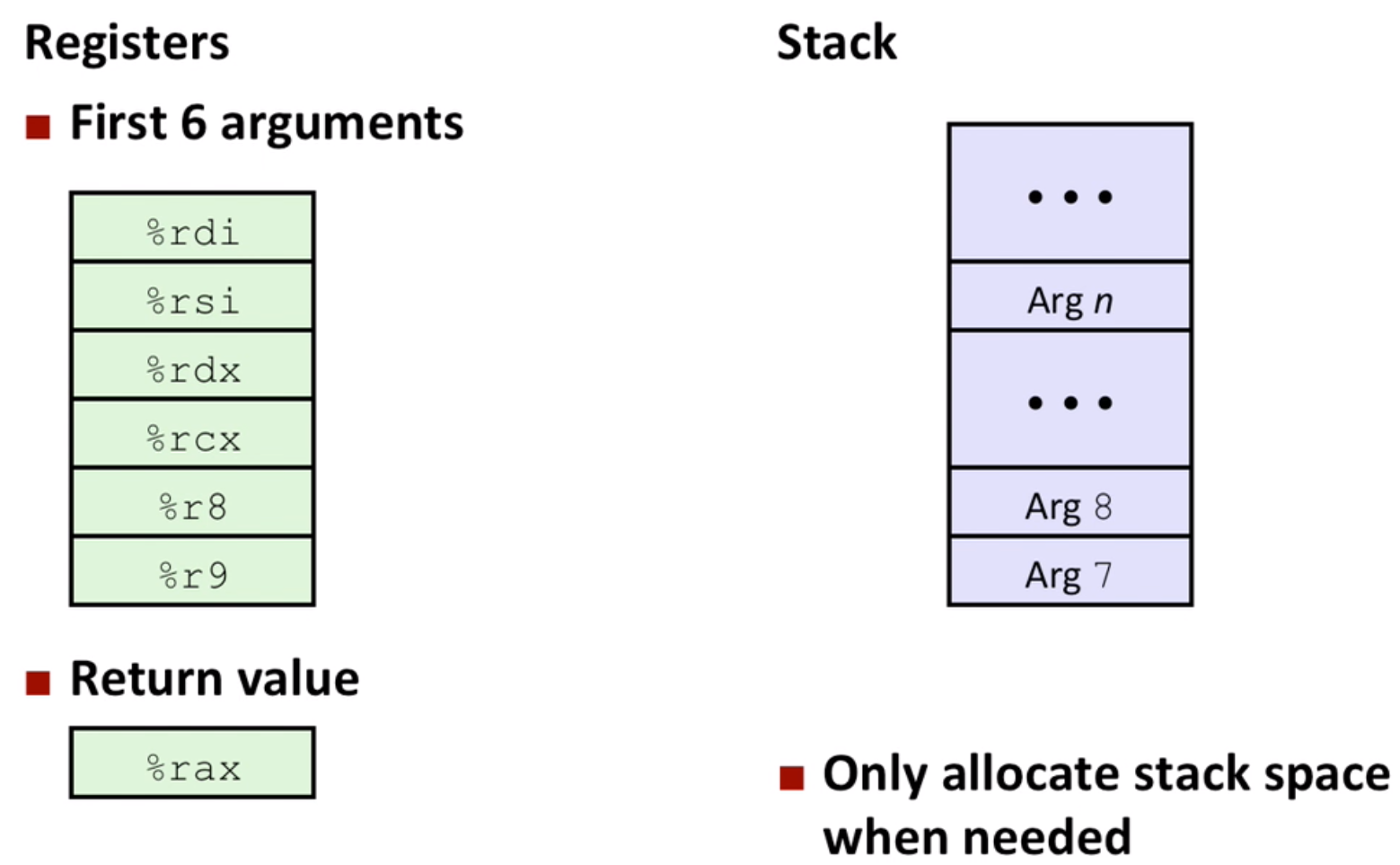
• save local data:

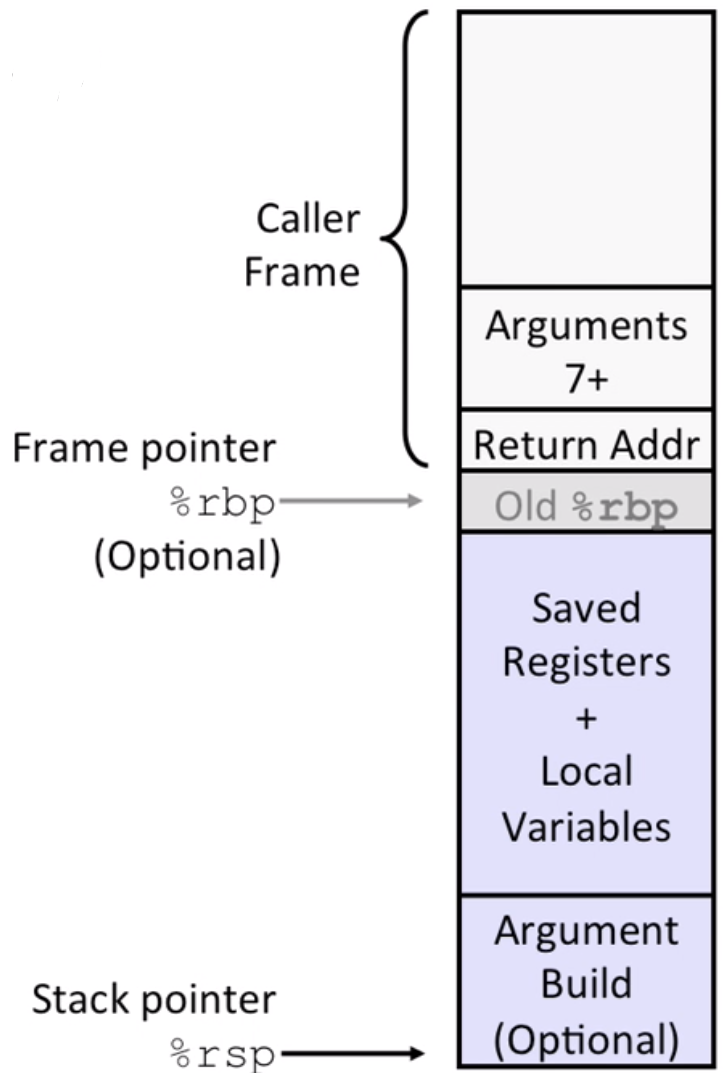
Normally, use %rsp directly, sub some value at the beginning, then add it back before return.

It’s OK to use movl to %esi, since the rest of 32 bits would be set to zero. This depends on the compiler

Sometimes use %rbp, like allocating an array or memory buffer

• Caller Saved and Callee Saved

Rules we need to obey, set in ABI(application binary interface)

caller saved: the register can be overwritten–%rax, all of the arguments from %rdi to %r9, tmp %r10 and %r11

callee saved: the callee make sure not to affect any data used in the caller–%rbx, from %r12 to %r14, %rbp and %rsp

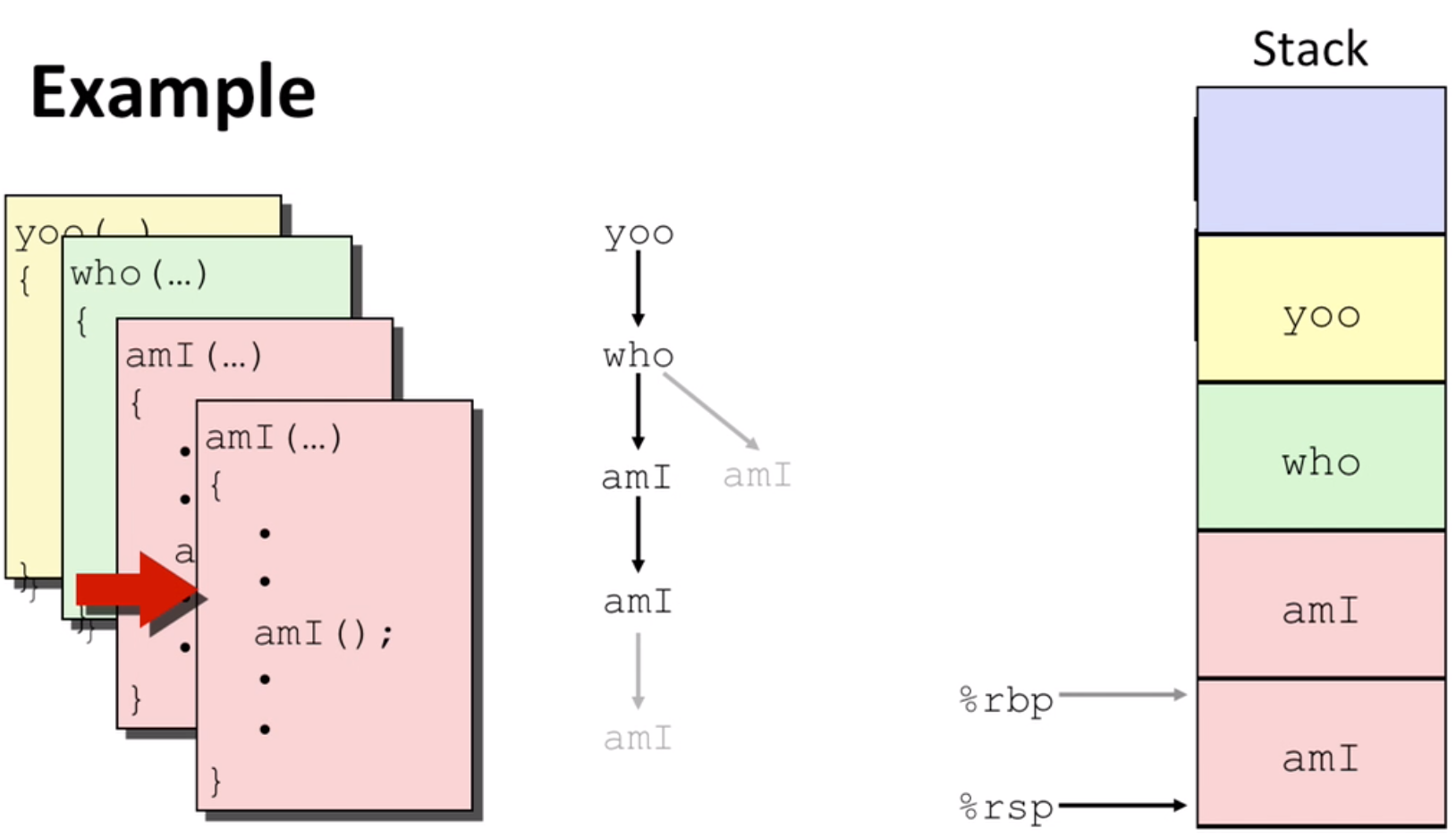
• recursive function example:

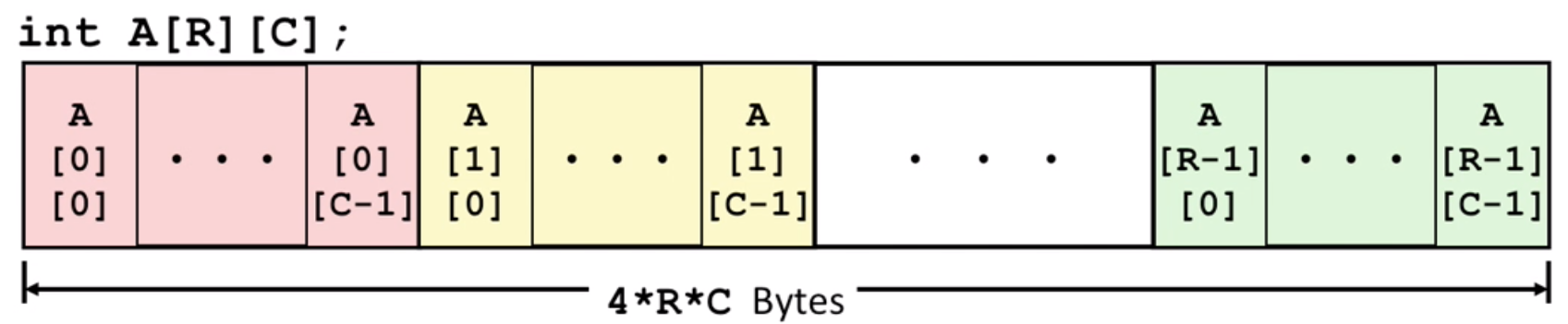
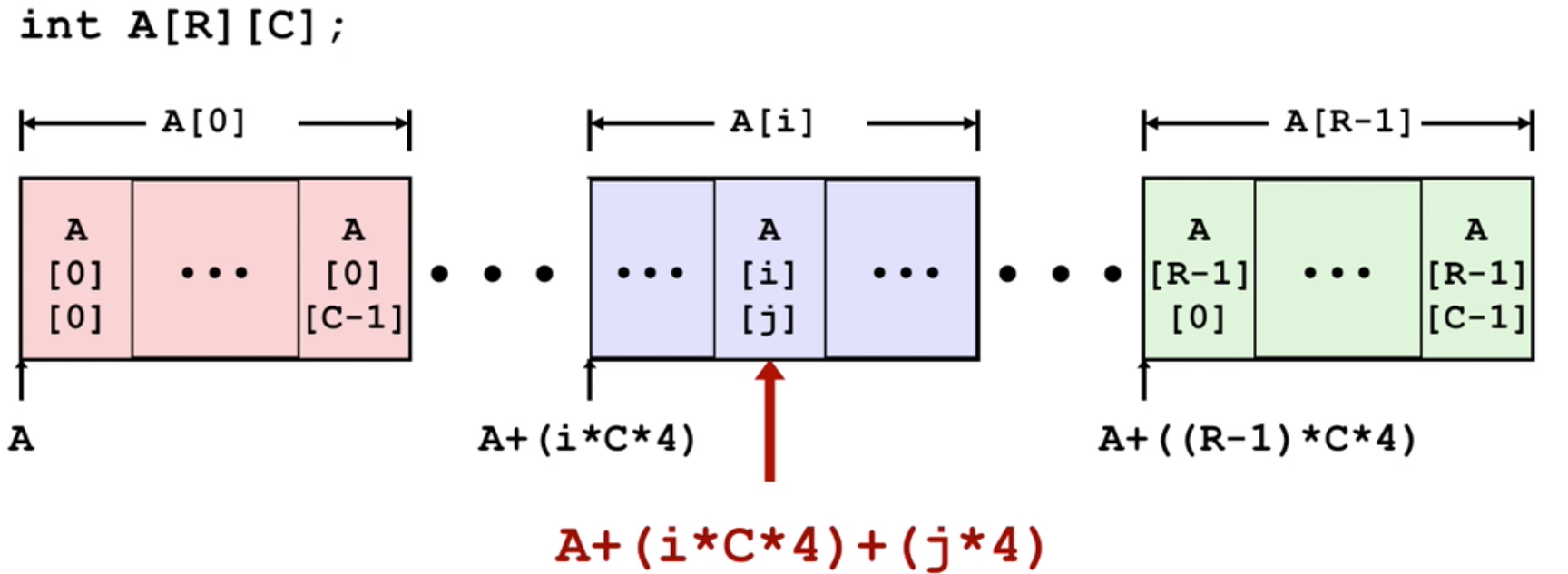
Arrays

Structures

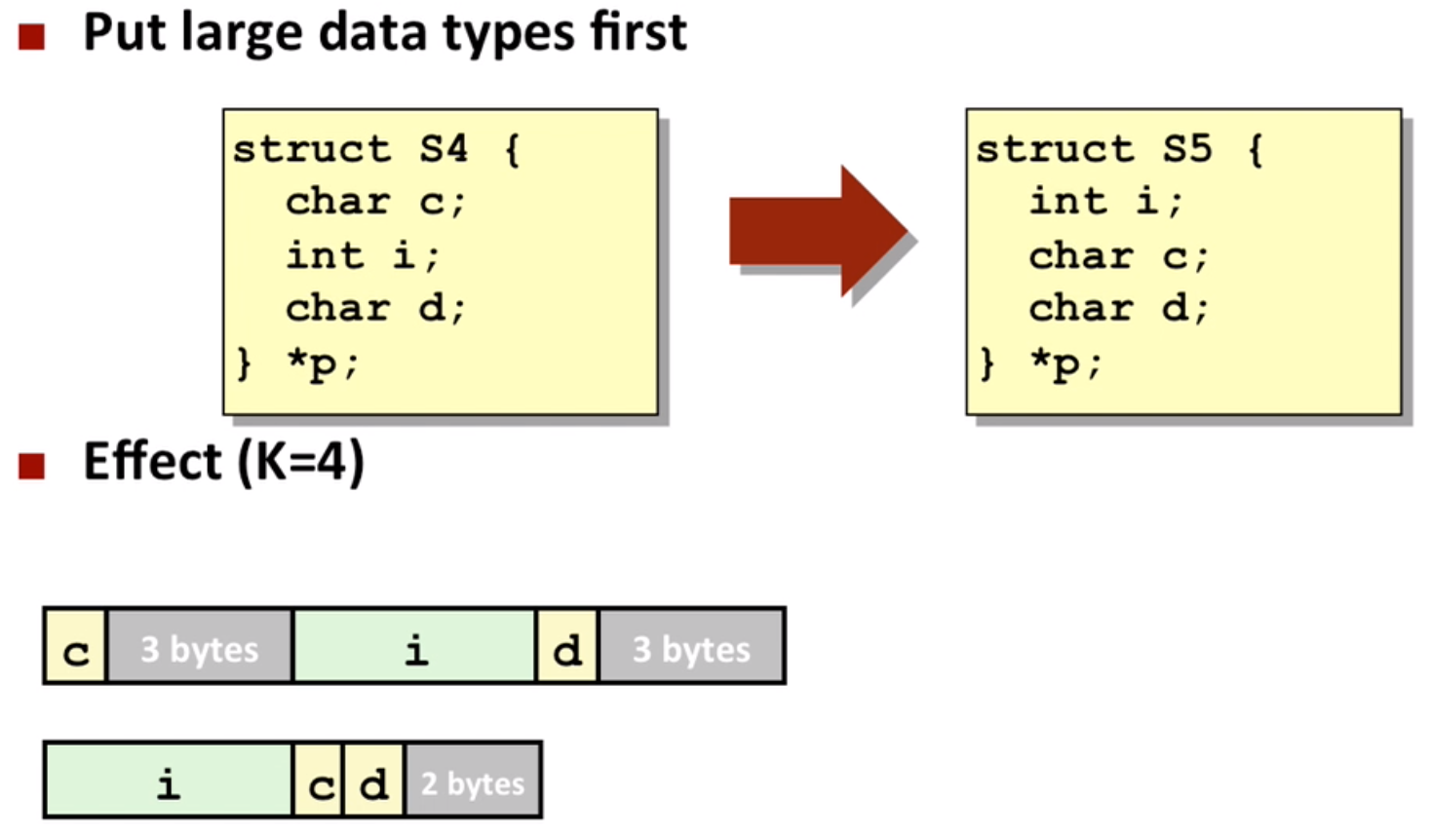
Floating Point

float add(param passed in %xmm0, %xmm1):

double add:

Memory Layout

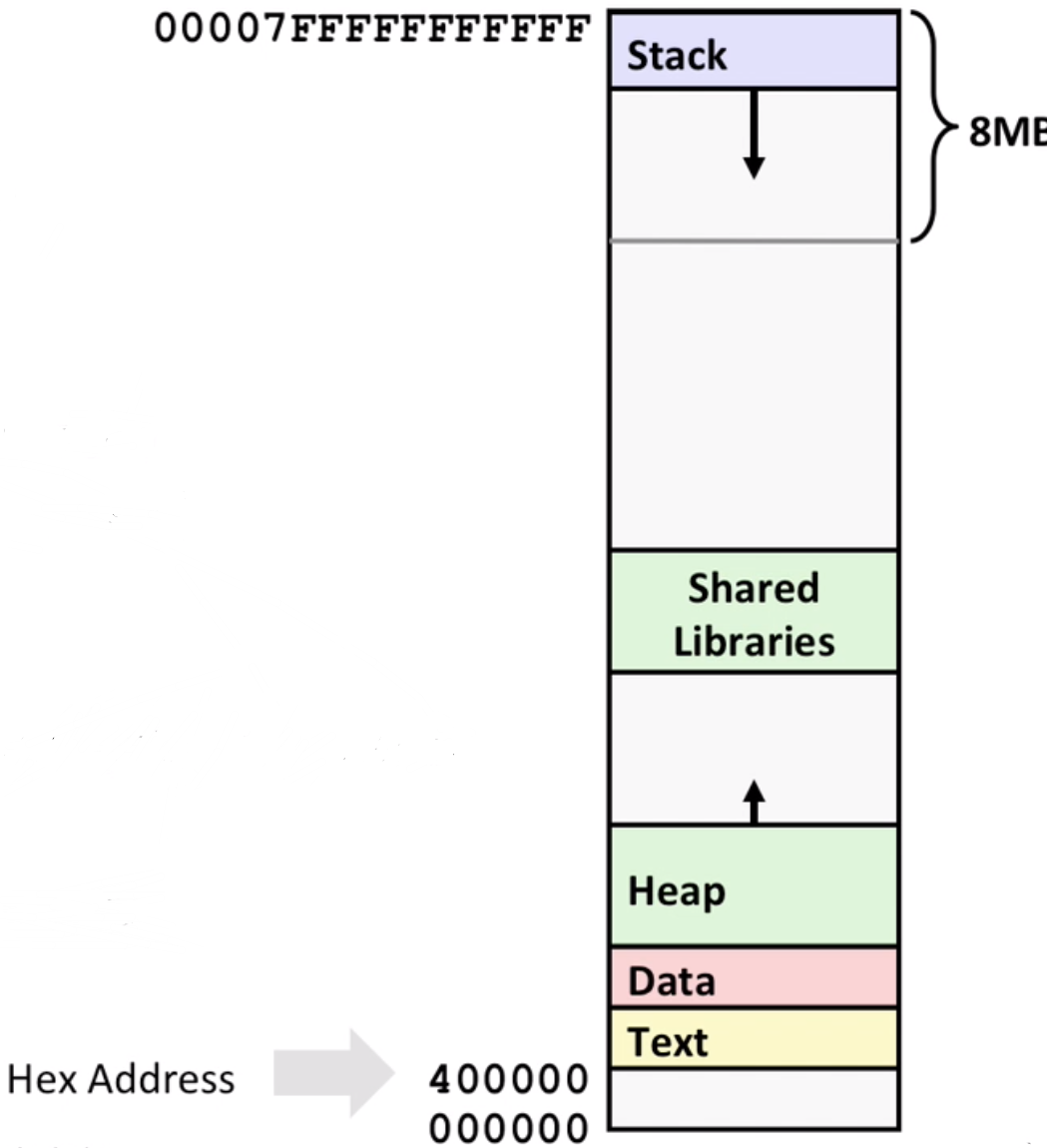
• stack for local variable (if more than 8MB, segmentation fault)
• heap memory is dynamically allocated for malloc、new …
• data is for static data
• Text/Shared Libraries for executable instructions(read only)

Buffer Overflow

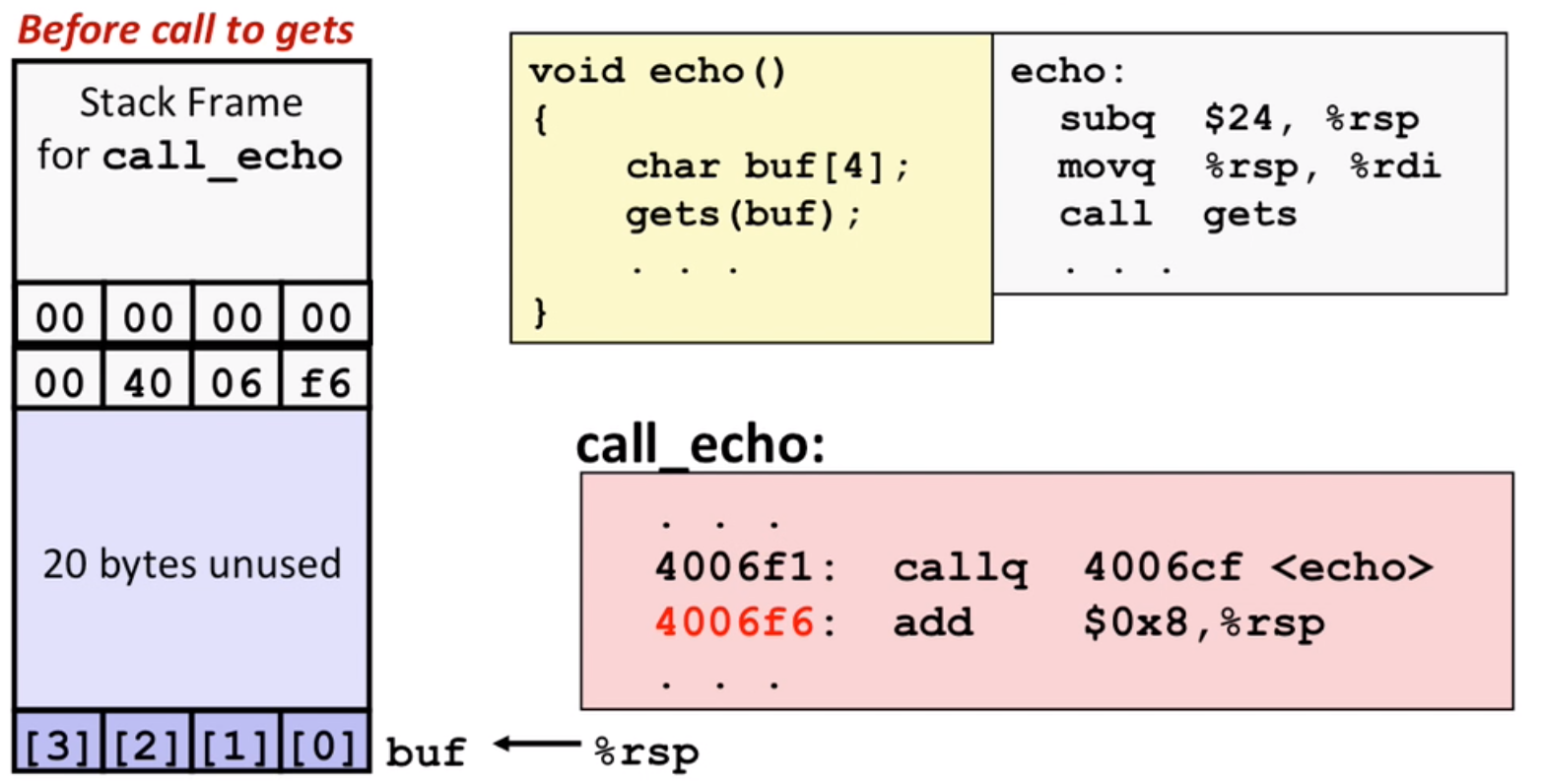
If you input 23 characters in gets(), it’s ok (a default \0 at the end of line)

If you put 24 characters or more, it will gets to the return address and may cause a segmentation fault(depends on the address you jump to)

code injection attacks

Covering the return address, and use the instruction we input (see attacklab for more details)

Ways to avoid:

• avoid overflow Vulnerabilities in Code:
  • fgets instead of gets
  • strncpy instead of strcpy
  • don’t use scanf with %s
• system-level protections
  • random stack offset: hard to predict the beginning of code
  • non-executable code segments: only execute the read-only memory instructions
• stack Canaries
  • save Canary in %rsp at first and then recheck it in the end(see bomblab for more details)

Return-Oriented Programming attacks

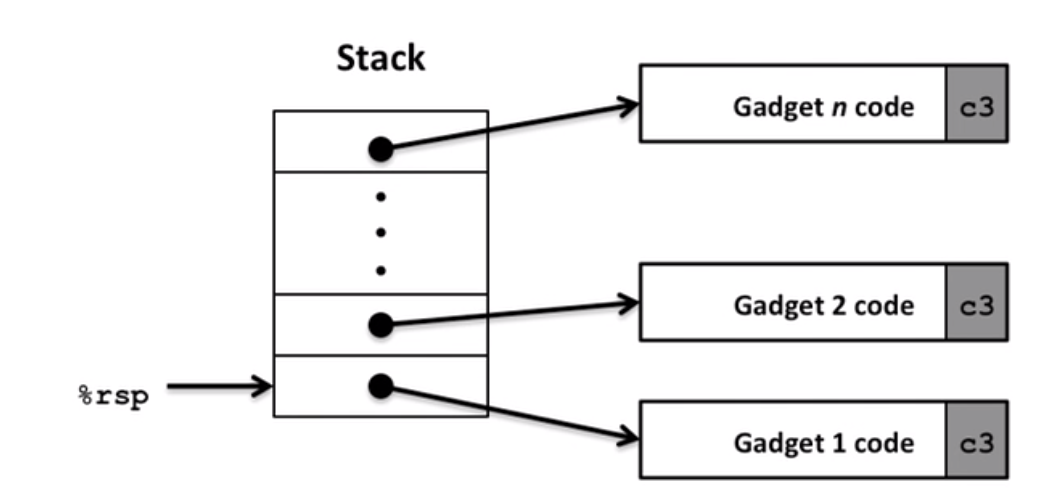
Use existing codes(gadgets) to attack, see attacklab for more details.